Що таке обернена задача?

Що таке обернена задача? 

Обернена задача – це задача, яка взаємопов’язана з іншою задачею сюжетом та числовими даними, але те, що в оберненій  задачі є шуканим, в іншій є даним, і навпаки. 

Розв’язуючи задачі, учні й учениці переконуються, що за допомогою математичних обчислень можна швидко вирішити багато життєвих практичних питань. Якщо ви прагнете, щоб дитина вміла добре розв’язувати задачі, навчіть її складати задачі, обернені до даної. 

Отож, обернена задача передбачає, що є інша задача, до якої ця задача є оберненою. Таку задачу називають прямою. Пряма та обернена задачі взаємообернені відносно одна одної. Пряму задачу зазвичай розв’язують першою, а обернену складають на її основі. 

Обернених задач може бути стільки, скільки числових даних в умові прямої задачі. Якщо задача на одну дію (проста), то обернених задач буде дві. Якщо задача на дві або більше дій (складена), то й обернених задач може бути більше.

Перш ніж вчитися складати та розв’язувати обернені задачі, дитина повинна бодай на початковому рівні:

• розуміти, що таке обернена арифметична дія та як пов’язані між собою пряма та обернена дії. Тобто дитина має знати, що віднімання є оберненою дією відносно додавання. А якщо учень чи учениця уже знайомі з множенням, то вони мають знати, що ділення є оберненою дією до множення;
• уміти обчислювати числові вирази; розуміти, як пов’язані між собою компоненти числового виразу та знати, як знайти невідомий компонент виразу, якщо відомі решта два. Наприклад, якщо відомі сума й один із доданків, то дитина має розуміти, як знайти другий доданок (від суми відняти відомий доданок), якщо відомі різниця та зменшуване – як знайти від’ємник (від зменшуваного відняти різницю) тощо;
• розуміти зв’язки між тими величинами, які відомі у прямій задачі, й шуканою величиною, і на основі цих даних уміти скласти числовий вираз із правильною арифметичною дією, за допомогою якої розв'язується задача. Тобто дитина має загалом розуміти, що таке задача і як її розв’язувати;
• бути ознайомленою з основними типами задач на одну дію: на знаходження суми, на  знаходження невідомого доданка, на знаходження різниці, на знаходження невідомого зменшуваного та від’ємника. 

Чому важливо складати обернені задачі?

Учитися складати та розв’язувати обернені задачі дуже важливо вже на етапі вивчення задач на одну дію, адже така діяльність допомагатиме дитині поглибити всі навички обчислення числових виразів та покращити розуміння нею взаємної оберненості арифметичних дій та зв'язків між їхніми компонентами.

Але найголовніше – складання обернених задач сприятиме розумінню дитиною молодшого шкільного віку спорідненості між усіма (відомими та невідомими) даними задачі. Дитина легко навчиться визначати правильний алгоритм розв’язування задач: розкладати будь-яку задачу на складові, перевіряти правильність її вирішення та й загалом бачити задачу як певний пазл-схему, із яким легко працювати. 

Отож, як навчити дитину складати та розв’язувати обернені задачі на одну дію? 

По-перше, учіть дитину правильно аналізувати та коротко записувати умову задачі. Дитина має добре розуміти, що в задачі є даним, а що слід знайти. Щоб дитина засвоїла, як це робити, скористайтеся добіркою готових завдань.

По-друге, привчайте дитину складати схему до задачі. Це можуть бути опорна схема-відрізок та табличка з усіма відомими й невідомими даними. Така наочність допоможе дитині швидко збагнути, як можна замінити шукане даним. 

Наприклад, у задачі на знаходження суми оберненими будуть задачі на визначення невідомих доданків. Ось як це можна пояснити дитині на прикладі прямої та оберненої задач на знаходження суми двох чисел.

Пряма задача: Андрій має 4 червоні машинки та 8 синіх. Скільки машинок в Андрія усього?

У цй задачі ми визначаємо суму. Вона позначена знаком питання на схемі. А в табличку записуємо відомі та невідомі дані.

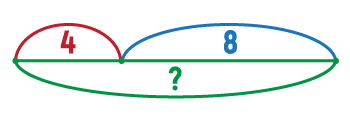
Задача розв’язується за допомогою числового виразу на знаходження суми.

4 + 8 = 12 (шт.)

Оберненими задачами до цієї прямої задачі будуть такі. 

Перша обернена задача: Андрій  має 10 машинок. Із них 4 червоні, решта – сині. Скільки синіх машинок має Андрій?

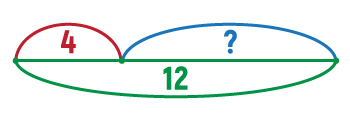
Обчислюємо цю обернену задачу за допомогою виразу на віднімання.

12 – 4 = 8 (шт.)

Друга обернена задача: Андрій має 10 машинок. Із них 8 сині, решта – червоні. Скільки червоних машинок має Андрій?

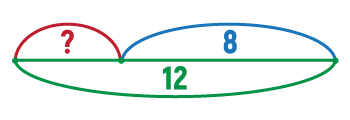
12 – 8 = 4 (шт.) 

В обернених задачах мовиться про того самого Андрія і його машинки. Ми знаємо, що всього машинок 12, і шукаємо невідомі доданки. Їх можна визначити на основі дії, оберненої до додавання. Від суми слід відняти відомий доданок. На схематичних зображеннях умови задачі видно, що пряма та обернені задачі взаємопов’язані й те, що є даним у прямій задачі, є шуканим в обернених. 

Щоб дитина швидше зрозуміла алгоритм складання таких обернених задач, намалюйте табличку з трьома однаковими комірками, куди запишіть усі числові дані задачі. До прикладу, у задачі про Андрія та його машинки числовими даними є 4, 8, 12.

Виріжте прямокутник відповідно до розміру комірки (бажано яскравого кольору) або ж скористайтеся підручним матеріалом відповідного до комірки розміру (кубик Lego, плаский камінець тощо) так, щоб можна було затулити число. Коли дитина розв’язуватиме пряму задачу на суму, затуліть 12. При складанні обернених задач затуляйте інші числа. Дитина наочно побачить, що обернені задачі створюються на основі тих самих даних. Ви можете зробити таку табличку-шаблон із ламінованого паперу й використовувати для складання різних обернених задач. 

Якщо прямою є задача на знаходження різниці (остачі), то оберненими будуть задачі на знаходження зменшуваного та від’ємника. Ось пряма задача. 

У корзині було 9 пиріжків. На обід діти з’їли 3 пиріжки. Скільки пиріжків залишилося в корзині?

Користуючись таблицею-підказкою, запишіть у неї усі дані та затуліть число 6 у третій комірці, щоб дитина не бачила відповіді. 

Коли задачу розв’язано, запропонуйте дитині затулити число 9 у таблиці й придумати обернену задачу з невідомим зменшуваним. Далі повторіть ці дії з невідомим від’ємником. Таку наочність використовуйте на початках. Згодом нехай дитина вчиться складати обернені задачі на основі короткого запису умови задачі без допомоги. Короткий запис задачі про Андрія та машинки має виглядати орієнтовно ось так.

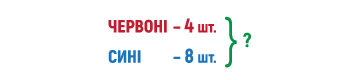
Короткі умови обернених задач виглядатимуть так само, але знак питання має бути на місці шуканого числа. 

Якщо дитина засвоїть алгоритм короткого запису задачі, це свідчитиме, що вона розуміє зв'язок між усіма даними, знає, який це тип задачі та за допомогою якого виразу можна знайти відповідь. Підкажіть синові чи доньці, що короткий запис – це  найважливіший опорний момент при розв’язанні задачі, на основі якого відразу видно, які дані в обернених задачах можуть стати шуканими. Продемонструйте дитині, як правильно змінювати умову задачі, як ставити запитання до оберненої задачі, як зрозуміти, скільки таких задач можна скласти до даної. Щоб дібрати найцікавіші задачі на одну дію, натискайте на посилання.

Як навчити дитину складати й розв’язувати обернені задачі до складених задач?

Щоб навчити дитину складати обернені задачі, давайте їй достатньо часу для засвоєння алгоритму на простих задачах одного виду (задачі на знаходження суми, різниці (остачі), збільшення та зменшення числа на кілька одиниць, різнецеве порівняння двох чисел, знаходження невідомого доданка). Згодом пропонуйте складати обернені задачі до задач на дві дії. У цих задачах правильний запис короткої умови та визначення плану дій є ще важливішими. У процесі розв'язання таких складених задач дитина має засвоїти, що всі обернені задачі вибудовуються за тією самою математичною структурою, яку можна простежити в короткому записі прямої задачі. Але якщо дитина вже в змозі скласти план розв’язання задачі на дві дії, то впорається і з оберненими задачами. Важливо пояснити їй, що короткий запис умови задачі – це опора при пошуку алгоритму розв’язування задачі. І якщо в короткому записі замінити знаком питання дані, то можна зрозуміти, яке питання до оберненої задачі треба поставити,  що у ній стає шуканим та скільки обернених задач можна скласти. Ось приклад короткого запису задачі:

До свята діти купили 54 смаколики. Морозива та шоколадок придбали 38 штук. А тістечок на 8 штук більше, ніж морозива. Скільки тістечок, морозива та шоколадок купили для свята?

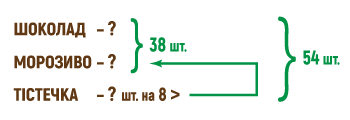
У короткому записі задачі маємо 3 знаки запитання. Якщо в умові інформацію про кількість морозива зробити відомою (30 шт.), а загальну кількість солодощів шуканою ( ? ), ми отримаємо обернену задачу. Таких обернених задач може бути щонайменше три.  

Складання обернених задач дуже добре потренує вміння розв’язувати задачі та навчить дітей самоперевірки. Окрім цього, така робота сприятиме розвитку логіки, гнучкості аналітичного мислення й уваги. 

Авторка: Наталка Бачко, фахівчиня з домашнього навчання