Як пояснити дитині дроби

Діти молодшого шкільного віку добре знайомі із числами та основними правилами, що з ними пов’язані. Діти знають, що в числовому ряду більше число завжди йде після меншого; число «1» позначає один предмет, а число «2» – два предмети. Але вивчення дробів може збентежити дитину, адже виявляється, що 1/2 – це більше, ніж 1/5, а 1/5 і 1/2 – менше, ніж 1. Те, що між 0 і 1 є ще якісь числа, здатне  здивувати дитину. До всього, дроби ще й виглядають незвично. Діти не розуміють: це одне число чи два? Тому пропонуємо кроки, що допоможуть пояснити дитині дроби цікаво й зрозуміло.

Як співвідносяться ціле та частини?

Починаючи вивчати дроби, дитина має добре розуміти, що таке частина цілого. Здатність співвідносити частину та ціле й розуміння того, що ціле може складатися із частин, формуються ще задовго до школи. Пригадайте, як захопливо ваш малюк у віці 1,5–2 років складав перші пазли. Тоді дитина як справжній дослідник відкривала для себе цікавий закон: із частинок може утворитися ціле, із маленьких незрозумілих квадратиків з'являється ціла картина. Ті самі відкриття очікують на дитину і при складанні конструкторів та мозаїк.

Окрім того, діти з найменшого віку спостерігають ситуації та випадки, коли ціле стає частинами. Листок паперу здатен розірватися (маленькі діти полюбляють рвати папір на шматки), банан – розламатися навпіл, а склянка може бути наповнена молоком тільки наполовину. Такі невимушені життєві ситуації знайомлять дитину  з діленням, закладаючи ґрунт для розуміння того, що одне (ціле) можна розділити. Цей досвід важливий для розуміння дробів.

Отож, перш ніж розповідати про чисельник та знаменник, поговоріть із дитиною про ціле та частини: половини, третини, четвертини.

Щоб зацікавити юних дослідника чи дослідницю, запропонуйте декілька непересічних запитань та здивуйте незвичною пропозицією. Наприклад, скажіть, що ви можете довести, що 2 може дорівнювати 1. Дитину, яка уже знайома з діленням, можна запитати, як 1 поділити на 2. Імовірно, вона добре замислиться. Міркуйте разом. Як розділити 2 яблука між 2-ма людьми? Звісно ж, це дуже просто. А якщо є лише 1 яблуко, а людей двоє? Ділимо на половинки. Це теж ніби просто, але є один цікавий нюанс. Яблуко було одне, а половинок дві. Ось ми й розділили 1 на 2. Дві половинки яблука дорівнюють 1 цілому яблуку. Запропонуйте дитині знайти та замалювати половинки різних фігур, розрізати навпіл папір, розділити печиво чи шоколад навпіл. А далі, поміркувавши, можна зробити такі висновки:

• половина – менша, ніж ціле;
• може бути тільки дві половини цілого, оскільки, якщо ціле розділити на більше частин, то це вже буде не половина, а третина чи четвертина тощо;
• не буває більшої чи меншої половини. Обидві половини рівні між собою. Тому їх можна назвати рівними частинами цілого.

Ці частини цілого – половини, третини тощо – позначаються особливими числами, які називаються дробами.

Що таке дроби?

Отож, дроби – це числа, які позначають рівні частини цілого. Ділити ціле можна не лише на половини, тобто на дві рівні частини. Можна ділити на три, чотири частини й так далі до нескінченності. І всі ці частинки будуть менші за одне ціле. Математичною мовою дроби записують за допомогою двох чисел та лінії, яка їх розділяє. Наприклад, половина – це 1/2, що означає, що це одна частина з двох. Третина, або 1/3 , – це одна частина з трьох, 1/6 означає, що це одна частина із шести.

Підкажіть дитині, що слово «дроби» близьке за звучанням до слова «дробити», тобто ділити. Дріб означає, що ціле (наприклад, торт) поділили на ту чи іншу кількість частин. Запропонуйте дитині уявити, що у вас свято (день народження улюбленої іграшки). Розсадіть кілька іграшкових звірят, запрошених на свято. Намалюйте та виріжте разом великий круглий торт. З’їсти його цілим не вийде, бо він занадто великий, тож доведеться ділити торт, та й гостей треба пригостити. При цьому важливо ділити на рівні частини (інакше буде нечесно і хтось може образитися). Гостей 4, значить, кожен отримає одну частинку із чотирьох, тобто 1/4 торта. Нехай дитина роздасть шматки торта гостям, пояснюючи кожному, що він отримав 1/4 торта.

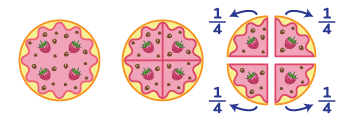
Надалі пропонуйте дитині схожі завдання, пов’язані з дробами, де в чисельнику 1. Завдяки цьому дитина зрозуміє суть поділу на частки. Такі дроби називають одиничними. Для цього:

• просіть дати вам 1/4 яблука чи 1/3 цукерки;
• пропонуйте завдання, де треба замалювати половину, третину чи  чверть фігури. Запитайте, як половину, третину та чверть записують дробами;
• виріжте з паперу декілька кругів і розріжте на рівні частини, щоб дитина мала змогу підписати кожну з них дробом;
• дайте завдання відрізати від одного шматка паперу 1/4, від іншого – 1/5. Допомагайте і підказуйте, оскільки вирахувати й відрізати рівну частину непросто;
• на кухні показуйте, що відрізали 1/3 огірка, готуючи салат, чи наповнили 1/2 склянки водою.

У нагоді стануть пластилін, нитки-шнурочки, папір, Lego, різноманітна їжа, яку можна ділити.

Після такої практики з ділення попросіть дитину розв’язати декілька задач, де треба вирахувати, скільки становитимуть третина, чверть, п’ята частина тощо від заданого числа. І навпаки – шукайте загальну кількість від заданої частини. Для цього скористайтеся готовим завданням. 

Що таке чисельник та знаменник?

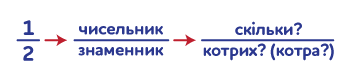
Поясніть дитині, що кількість частин, на які були розділені торт, яблуко, круг, шоколадка тощо (усе те, що ви ділили та різали разом), називається знаменником. Знаменник записується під лінією і позначає, на скільки частин поділене ціле. Верхнє число в дробі називається чисельником. Воно позначає, скільки частин цілого взяли. Щоб дитина запам’ятала, де знаменник, а де чисельник, запропонуйте таку підказку: «Знаменник – з, знизу. Він відповідає на питання «котрих?», «котра?». Чисельник відповідає на питання «скільки?».

Іноді є потреба взяти більше, ніж 1 шматок торта. Наприклад, 2 шматки з 8, тобто 2/8. 

Щоб закріпити розуміння дитиною звичайних дробів, пропонуйте їй цікаві завдання:

• вивчати дроби за допомогою шматочків піци;
• замалювати необхідну кількість частин фігури відповідно до вказаного дробу;
• шукати частини незвичних фігур;
• виконати тестове завдання і позначити дріб, зображений на малюнку; 
• наповнити склянки, намалювавши потрібну кількість соку в кожній із них;
• шукати дроби на числовій осі.

Варто зауважити, що дитина має шукати дроби та позначати необхідну кількість частин на різних типах фігур та відрізків. Окрім того, слід пояснити, що ціле – це не завжди лише один предмет. Іноді за ціле можна взяти групу предметів, наприклад, мішечок із цукерками чи групу звірят, яку теж можна вважати умовним цілим.

Для усвідомлення таких особливостей дробів чудово підійдуть завдання, де треба один і той самий дріб позначити різними способами, а також завдання на позначення необхідної кількості предметів у групі відповідно до дробу.

Також важливо виконувати й обернені завдання, щоб дитина за малюнком визначала потрібний дріб.

Як знайти дріб від числа?

Є правило: щоб знайти дріб від числа, треба це число розділити на знаменник і результат помножити на чисельник. Тобто знаменник вказує, на скільки частин ми будемо ділити число, а чисельник – скільки із цих частин ми маємо взяти. До прикладу, якщо є завдання знайти 3/5 від 125, то слід 125 розділити на 5 і помножити на 3.

1. 125 : 5 = 5;
2. 5 · 3 = 15.

Буває, що учням складно запам’ятати, на що ділити, а на що множити. Зверніть увагу дитини, що риска в дробі означає те  саме, що й ділення. І знаменник – це, по суті, дільник, тобто те число, на яке треба ділити. Якщо школяр усвідомить залежність знаменника та дії ділення, він завжди знатиме, що ділять на знаменник. Удосконалити вміння знаходити дріб від числа можна, виконуючи різні завдання та цікаві задачі.

Які основні властивості дробів?

Дроби, як і натуральні числа, можна порівнювати, додавати, віднімати тощо. Але для цього треба знати їхні основні секрети.

Ознайомте дитину з основною властивістю дробів: якщо чисельник і знаменник помножити або поділити на те саме число, то значення дробу не зміниться. Почати пояснення варто з еквівалентних дробів. Еквівалентні дроби – це ті, які позначають ту саму частину цілого, навіть якщо не мають однакових чисельників та знаменників. 

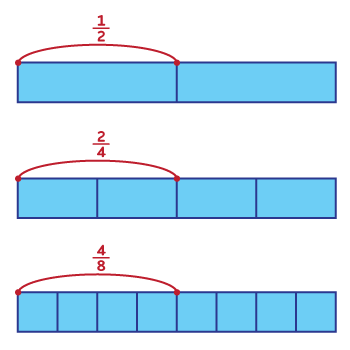
Усвідомити таку властивість дробів може бути непросто для дитини. Тому слід на цьому етапі багато візуалізувати. Корисно вирізати два однакові круги (нехай це будуть піца чи торт, які дитина розмалює на власний розсуд) і разом із нею розділити один круг навпіл, а інший – на чотири частини. Дайте дитині змогу маніпулювати усіма цими шматочками, накладаючи четвертинки на половинки.

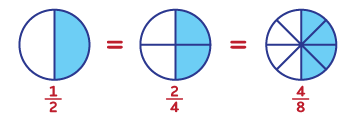
 1/2,  2/4,  4/8  – це дроби,  рівні між собою, оскільки позначають  ту саму частину торта.

Нехай дитина виконає завдання, де доведеться наочно переконатися, що замальовані частини рівні, навіть  якщо фігура поділена на різні частини.

Таких завдань варто зробити багато, оскільки засвоєння властивості дробів про рівність важливе для подальшого розуміння, як порівнювати, додавати, множити та ділити дроби. Для цього скористайтеся комплектом завдань «Рівність дробів». Виконавши завдання цього комплекту, дитина зрозуміє, як порівнювати дроби з однаковими знаменниками та еквівалентні дроби. Згодом пропонуйте складніше завдання, де на основі розуміння основної властивості дробів дитині треба вписати чисельник чи знаменник. 

Розкажіть про дроби, які дорівнюють одиниці, та дроби, більші за одиницю.

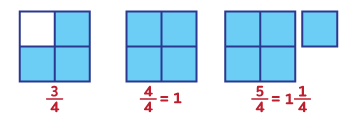
Дріб, у якого і в чисельнику, і в знаменнику однакове число, дорівнює одиниці. Дріб, у якого чисельник більший за знаменник, більший від 1.

Для візуалізації намалюйте та покажіть дитині такий відрізок.

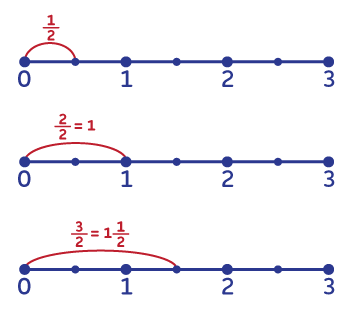
Слід розуміти, що вивчення дробів має ускладнюватися відповідно до віку дитини. З молодшими школярами можна робити нескладні операції на додавання та порівняння дробів. Але це тема, яка досліджується впродовж років. Вона справді непроста, хоча й надзвичайно цікава. Щоб у майбутньому дитина не відчувала труднощів при складніших операціях із дробами, варто докласти зусиль зараз, у початковій школі. Багато візуалізуйте та пояснюйте. Вивчення дробів може бути захопливим, а іноді навіть смачним.

Авторка: Наталка Бачко, фахівчиня з домашнього навчання