Наприклад: периметр прямокутника 3 клас
Порівняння дробів
(25)-
 Учимось порівнювати правильні й неправильні звичайні дроби № 1Завдання, що допоможе дитині навчитись порівнювати дроби та розташовувати їх у порядку зростання – від меншого до більшогоЗАВАНТАЖИТИ
Учимось порівнювати правильні й неправильні звичайні дроби № 1Завдання, що допоможе дитині навчитись порівнювати дроби та розташовувати їх у порядку зростання – від меншого до більшогоЗАВАНТАЖИТИ -
 Тренувальне завдання «Рівні дроби»Завдання, що сприятиме кращому засвоєнню поняття звичайних дробів та їх основної властивості, а також розвиватиме математичне мисленняЗАВАНТАЖИТИ
Тренувальне завдання «Рівні дроби»Завдання, що сприятиме кращому засвоєнню поняття звичайних дробів та їх основної властивості, а також розвиватиме математичне мисленняЗАВАНТАЖИТИ -
 Вивчаємо основну властивість дробу № 1Завдання, що допоможе дитині наочно вивчити поняття рівності дробів, застосовуючи зорову та м’язову пам’ять і тренуючи математичне мисленняЗАВАНТАЖИТИ
Вивчаємо основну властивість дробу № 1Завдання, що допоможе дитині наочно вивчити поняття рівності дробів, застосовуючи зорову та м’язову пам’ять і тренуючи математичне мисленняЗАВАНТАЖИТИ -
 Учимося показувати дроби на малюнкахЗавдання сприятиме формуванню математичної компетентності дітей, уявлення про дріб як частину цілогоЗАВАНТАЖИТИ
Учимося показувати дроби на малюнкахЗавдання сприятиме формуванню математичної компетентності дітей, уявлення про дріб як частину цілогоЗАВАНТАЖИТИ -
 Вивчаємо основну властивість дробуКомплект завдань, що допоможе дитині наочно вивчити поняття рівності дробів, застосовуючи зорову та м’язову пам’ять та тренуючи математичне мисленняЗАВАНТАЖИТИ
Вивчаємо основну властивість дробуКомплект завдань, що допоможе дитині наочно вивчити поняття рівності дробів, застосовуючи зорову та м’язову пам’ять та тренуючи математичне мисленняЗАВАНТАЖИТИ -
 Учимось порівнювати правильні й неправильні звичайні дробиКомплект завдань, що допоможе дитині навчитись порівнювати дроби та розташовувати їх у порядку зростання – від меншого до більшогоЗАВАНТАЖИТИ
Учимось порівнювати правильні й неправильні звичайні дробиКомплект завдань, що допоможе дитині навчитись порівнювати дроби та розташовувати їх у порядку зростання – від меншого до більшогоЗАВАНТАЖИТИ -
 Вивчаємо дроби цікавоЗавдання для формування математичної компетентності, удосконалення розуміння способу одержання дробуЗАВАНТАЖИТИ
Вивчаємо дроби цікавоЗавдання для формування математичної компетентності, удосконалення розуміння способу одержання дробуЗАВАНТАЖИТИ -
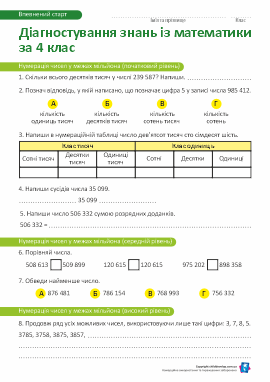 Банк завдань для діагностування освітніх втрат із математики в учнів 5 класу (за 4 клас)Завдання для діагностування освітніх втрат із математики перед початком навчання у 5-му класі. Перевірка знань за 4-й клас із математикиЗАВАНТАЖИТИ
Банк завдань для діагностування освітніх втрат із математики в учнів 5 класу (за 4 клас)Завдання для діагностування освітніх втрат із математики перед початком навчання у 5-му класі. Перевірка знань за 4-й клас із математикиЗАВАНТАЖИТИ -
 Вивчаємо основну властивість дробу № 4Завдання, що допоможе дитині наочно вивчити поняття рівності дробів, застосовуючи зорову пам’ять і тренуючи математичне мисленняЗАВАНТАЖИТИ
Вивчаємо основну властивість дробу № 4Завдання, що допоможе дитині наочно вивчити поняття рівності дробів, застосовуючи зорову пам’ять і тренуючи математичне мисленняЗАВАНТАЖИТИ -
 Частини цілого - діагностувальна робота 3 класЗавдання для формування математичної компетентності, удосконалення вміння підсумовувати та узагальнювати вивченеЗАВАНТАЖИТИ
Частини цілого - діагностувальна робота 3 класЗавдання для формування математичної компетентності, удосконалення вміння підсумовувати та узагальнювати вивченеЗАВАНТАЖИТИ -
 Вивчаємо дроби на майстер-класіЗавдання для формування математичної компетентності, удосконалення вміння застосовувати правило знаходження дробу під час розв’язування практично зорієнтованих завданьЗАВАНТАЖИТИ
Вивчаємо дроби на майстер-класіЗавдання для формування математичної компетентності, удосконалення вміння застосовувати правило знаходження дробу під час розв’язування практично зорієнтованих завданьЗАВАНТАЖИТИ -
 Учимось порівнювати правильні й неправильні звичайні дроби № 2Завдання, що допоможе дитині навчитись порівнювати дроби та розташовувати їх у порядку зростання – від меншого до більшогоЗАВАНТАЖИТИ
Учимось порівнювати правильні й неправильні звичайні дроби № 2Завдання, що допоможе дитині навчитись порівнювати дроби та розташовувати їх у порядку зростання – від меншого до більшогоЗАВАНТАЖИТИ -
 Вивчаємо основну властивість дробу № 7Завдання, що допоможе дитині наочно вивчити поняття рівності дробів, застосовуючи зорову пам’ять і тренуючи математичне мисленняЗАВАНТАЖИТИ
Вивчаємо основну властивість дробу № 7Завдання, що допоможе дитині наочно вивчити поняття рівності дробів, застосовуючи зорову пам’ять і тренуючи математичне мисленняЗАВАНТАЖИТИ -
 Вивчаємо основну властивість дробу № 2Завдання, що допоможе дитині наочно вивчити поняття рівності дробів, застосовуючи зорову та м’язову пам’ять і тренуючи математичне мисленняЗАВАНТАЖИТИ
Вивчаємо основну властивість дробу № 2Завдання, що допоможе дитині наочно вивчити поняття рівності дробів, застосовуючи зорову та м’язову пам’ять і тренуючи математичне мисленняЗАВАНТАЖИТИ -
 Вивчаємо основну властивість дробу № 9Завдання, що допоможе дитині наочно вивчити поняття рівності дробів, застосовуючи зорову пам’ять і тренуючи математичне мисленняЗАВАНТАЖИТИ
Вивчаємо основну властивість дробу № 9Завдання, що допоможе дитині наочно вивчити поняття рівності дробів, застосовуючи зорову пам’ять і тренуючи математичне мисленняЗАВАНТАЖИТИ -
 Вивчаємо основну властивість дробу № 3Завдання, що допоможе дитині наочно вивчити поняття рівності дробів, застосовуючи зорову та м’язову пам’ять і тренуючи математичне мисленняЗАВАНТАЖИТИ
Вивчаємо основну властивість дробу № 3Завдання, що допоможе дитині наочно вивчити поняття рівності дробів, застосовуючи зорову та м’язову пам’ять і тренуючи математичне мисленняЗАВАНТАЖИТИ -
 Учимось порівнювати звичайні дроби № 3Завдання, що допоможе дитині навчитись порівнювати дроби та розташовувати їх у порядку зростання – від меншого до більшогоЗАВАНТАЖИТИ
Учимось порівнювати звичайні дроби № 3Завдання, що допоможе дитині навчитись порівнювати дроби та розташовувати їх у порядку зростання – від меншого до більшогоЗАВАНТАЖИТИ -
 Вивчаємо основну властивість дробу № 8Завдання, що допоможе дитині наочно вивчити поняття рівності дробів, застосовуючи зорову пам’ять і тренуючи математичне мисленняЗАВАНТАЖИТИ
Вивчаємо основну властивість дробу № 8Завдання, що допоможе дитині наочно вивчити поняття рівності дробів, застосовуючи зорову пам’ять і тренуючи математичне мисленняЗАВАНТАЖИТИ -
 Учимось порівнювати правильні й неправильні звичайні дроби № 5Завдання, що допоможе дитині навчитись порівнювати дроби та розташовувати їх у порядку зростання – від меншого до більшогоЗАВАНТАЖИТИ
Учимось порівнювати правильні й неправильні звичайні дроби № 5Завдання, що допоможе дитині навчитись порівнювати дроби та розташовувати їх у порядку зростання – від меншого до більшогоЗАВАНТАЖИТИ -
 Вивчаємо основну властивість дробу № 5Завдання, що допоможе дитині наочно вивчити поняття рівності дробів, застосовуючи зорову пам’ять і тренуючи математичне мисленняЗАВАНТАЖИТИ
Вивчаємо основну властивість дробу № 5Завдання, що допоможе дитині наочно вивчити поняття рівності дробів, застосовуючи зорову пам’ять і тренуючи математичне мисленняЗАВАНТАЖИТИ -
 Учимось порівнювати звичайні дроби № 4Завдання, що допоможе дитині навчитись порівнювати дроби та розташовувати їх у порядку зростання – від меншого до більшогоЗАВАНТАЖИТИ
Учимось порівнювати звичайні дроби № 4Завдання, що допоможе дитині навчитись порівнювати дроби та розташовувати їх у порядку зростання – від меншого до більшогоЗАВАНТАЖИТИ -
 Учимось порівнювати звичайні дроби № 8Завдання, що допоможе дитині навчитись порівнювати дроби та розташовувати їх у порядку зростання – від меншого до більшогоЗАВАНТАЖИТИ
Учимось порівнювати звичайні дроби № 8Завдання, що допоможе дитині навчитись порівнювати дроби та розташовувати їх у порядку зростання – від меншого до більшогоЗАВАНТАЖИТИ -
 Вивчаємо основну властивість дробу № 6Завдання, що допоможе дитині наочно вивчити поняття рівності дробів, застосовуючи зорову пам’ять і тренуючи математичне мисленняЗАВАНТАЖИТИ
Вивчаємо основну властивість дробу № 6Завдання, що допоможе дитині наочно вивчити поняття рівності дробів, застосовуючи зорову пам’ять і тренуючи математичне мисленняЗАВАНТАЖИТИ -
 Учимось порівнювати правильні й неправильні звичайні дроби № 6Завдання, що допоможе дитині навчитись порівнювати дроби та розташовувати їх у порядку зростання – від меншого до більшогоЗАВАНТАЖИТИ
Учимось порівнювати правильні й неправильні звичайні дроби № 6Завдання, що допоможе дитині навчитись порівнювати дроби та розташовувати їх у порядку зростання – від меншого до більшогоЗАВАНТАЖИТИ
Мистецтво порівняння: дроби як ключ до розуміння частин
Поняття дробу — фундаментальне у математиці, воно відкриває двері до розуміння не лише цілих чисел, а й частин цілого. Здатність ефективно виконувати порівняння дробів є критично важливою навичкою, необхідною для вирішення широкого спектра задач у математиці, фізиці, інженерії й навіть у повсякденному житті. Від вимірювання кількості інгредієнтів у рецепті до розподілу ресурсів у проєкті — дроби оточують нас всюди, і вміння їх порівнювати дозволяє приймати обґрунтовані й раціональні рішення. Порівняння дробів — інструмент для розуміння відношень і пропорцій, що лежать в основі багатьох явищ навколишнього світу. Навчальна платформа РОЗВИТОК ДИТИНИ пропонує інтерактивні інструменти та ресурси для опанування цього важливого уміння.
Алгоритми порівняння дробів
Почнемо з найпростішого випадку: порівняння дробів з однаковими знаменниками. У такій ситуації порівняння дробів зводиться до простого порівняння їхніх чисельників. Дріб з більшим чисельником буде більшим за дріб з меншим чисельником, якщо знаменники однакові.
Проте, коли знаменники різні, процес стає складнішим. Щоб порівняти дроби з різними знаменниками, необхідно спочатку привести їх до спільного знаменника. Спільний знаменник — це число, яке ділиться без остачі на обидва знаменники. Найчастіше використовується найменше спільне кратне (НСК) знаменників. Після знаходження НСК кожен дріб перетворюється таким чином, щоб його знаменник дорівнював НСК. Це досягається множенням чисельника і знаменника кожного дробу на відповідний множник. Важливо пам'ятати, що множення чисельника і знаменника на одне і те ж число не змінює значення дробу, а лише змінює його вигляд. Після приведення дробів до спільного знаменника порівняння дробових чисел знову зводиться до порівняння їхніх чисельників. Дріб з більшим чисельником буде більшим.
Розглянемо приклад: порівняти дроби 3/4 і 5/6. НСК знаменників 4 і 6 дорівнює 12. Перетворюємо дроби: 3/4 = (3 × 3) / (4 × 3) = 9/12 і 5/6 = (5 × 2) / (6 × 2) = 10/12. Тепер, порівнюючи 9/12 і 10/12, бачимо, що 10/12 більше, отже 5/6 > 3/4.
Існує альтернативний метод, який дозволяє порівняти дроби, не приводячи їх до спільного знаменника — метод “перехресного множення”. Суть цього методу полягає в тому, щоб помножити чисельник першого дробу на знаменник другого дробу і чисельник другого дробу на знаменник першого дробу. Результати цих множень порівнюються. Якщо результат множення чисельника першого дробу на знаменник другого дробу більший, ніж результат множення чисельника другого дробу на знаменник першого дробу, то перший дріб більший за другий.
Наприклад, знову порівняємо дроби 3/4 і 5/6. 3 × 6 = 18 і 5 × 4 = 20. Оскільки 20 > 18, то 5/6 > 3/4.
Порівняйте дроби: від теорії до практики
Ось декілька порад, які можуть спростити процес порівняння дробів:
- спрощення дробів: перед тим, як порівняти дроби, переконайтеся, що вони спрощені до найменшого вигляду;
- візуалізація: уявіть собі дроби як частини цілого (наприклад, піци), що може допомогти вам інтуїтивно зрозуміти, який дріб більший;
- перетворення в десяткові дроби: перетворіть звичайні дроби в десяткові дроби, виконавши ділення чисельника на знаменник, адже порівняння десяткових дробів часто є простішим, ніж порівняння звичайних дробів;
- оцінка відносно 1/2: порівняйте кожен дріб з ½ (якщо один дріб менший за 1/2, а інший — більший, то більший дріб очевидно більший);
- розпізнавання простих випадків: будь-який дріб з чисельником, рівним знаменнику, дорівнює 1, будь-який дріб з чисельником, меншим за знаменник, менший за 1, а будь-який дріб з чисельником, більшим за знаменник, більший за 1;
- порівняння з еталонними дробами: використовуйте дроби, значення яких ви добре знаєте (наприклад, 1/4, 1/3, 1/2, 3/4) як еталони для порівняння інших дробів.
Практика — ключ до засвоєння будь-якої математичної концепції, і порівняння дробів не є винятком. Розв’язуючи різноманітні задачі, ви не лише закріплюєте теоретичні знання, а й розвиваєте інтуїтивне розуміння дробів. Сайт childdevelop.com.ua пропонує широкий спектр ресурсів для допомоги у навчанні та розвитку. Кожен крок, навіть найменший, наближає вас до мети.
- Дошкільнята завдання
- Українська українська мова четвертий клас
- Математики 1 клас
- Українська абетка
- Англійська буква е
- Вправи на логічне мислення
- Логічні завдання для дітей 5 років
- Визначити час за годинником
- Урок малювання 2 клас
- Карточки для читання по складах
- Вивчення таблички множення
- Картки для вивчення англійської мови для дітей
- Розмальовки тварин для 1 класу
- Англійська мова для 4 років – Літера D
- Англійська мова для 6 років – Літера R
- Додавання в межах 10 для 3 класу
- Математика для 4 років – Фігури в об’єктах
- Фразеологізми для дітей 6-7 років (1 клас)
- Омоніми для дітей 6-7 років (1 клас)
- Учимося описувати місця – завдання для 3 класу
- Малювання однією лінією для четвертого класу
- Загальні компетенції для 3 років – Малюємо листівку
- Загальні компетенції для 5 років – Малюємо листівку
- Логіка для 4 років – Частини цілого
- Знайди доданки чисел від 1 до 10: переставний закон додавання
- Барвисті рими №3
- Кольорові сни інопланетянина
- Доповни сюжет малюнка № 9
- Розмальовка «Вчимо таблицю множення на 8»
- Учимось визначати перші літери слів № 6
- Знайди зайве слово №4: прикметники
- Визначаємо ознаки здоров’я
- Малюємо асоціації та розвиваємо фантазію №2
- Знайди доданки в межах 100
- Домальовуємо силуети №7
- Бабусині антоніми: пишемо текст
- Проводимо опитування батьків дитини
- Шукаємо назви малюнків на літеру «M» (англійська мова)
- Відрізняємо реальні факти від вигадок № 3
- Відрізняємо реальні факти від вигадок про тварин
- Порівнюємо й малюємо персонажів: Котигорошко й Змій
- Що готує бабуся: знайомимось із рецептами страв
- Розкажи без підготовки про незвичні літні канікули: продовжуємо розповідь
- Піратська карта: визначаємо місцеположення
- Математичне доміно: додавання двоцифрових чисел
- Задзеркалля: удосконалюємо навички читання
- Словник транспортних засобів: формуємо орфографічну грамотність
- Дикі тварини Африки – картки Домана
- Практичні завдання
- Англійська мова для дітей
- Англійський алфавіт для дітей
- Англійська мова: словниковий запас
- Я досліджую світ
- Українська мова та читання для дітей
- Вчимось писати речення - завдання для дітей
- Частини мови та правопис
- Літературне читання для дітей
- Учимося описувати – завдання для дітей
- Математика для дітей
- Множення та ділення
- Віднімання та додавання
- Задачі з математики для дітей
- Вчимося рахувати та писати цифри
- Порівняння чисел для дітей
- Вивчення дробів
- Розвиток дрібної моторики у дітей
- Аплікації для дітей
- Поробки для дітей
- Розвиток загальних компетенцій дитини
- Малювання для дітей
- Розмальовки для дітей
- Тематичні завдання для дітей
- Український алфавіт для дітей
- Завдання на логіку для дітей
- Практичні завдання
- Завдання для підготовки до школи
- Завдання для дітей 6-7 років (1 клас)
- Завдання для дітей 7-8 років (2 клас)
- Завдання для дітей 8-9 років (3 клас)
- Завдання для дітей 9-10 років (4 клас)
- Завдання для дошкільників
- Практичні завдання 2 роки
- Практичні завдання 3 роки
- Практичні завдання 4 роки
- Практичні завдання 5 років
- Практичні завдання 6 років
- Англійська мова для дітей
- Граматика англійської мови для дітей
- Кросворди англійською для дітей
- Головоломки англійською для дітей
- Англійська мова: іменник
- Англійська мова: дієслова
- Англійська мова: займенники
- Англійська мова: прикметники
- Англійська мова: числівники
- Англійська мова: артикль a / an
- Present Simple для дітей
- Present Continuous для дітей
- Past Simple для дітей
- Future Simple для дітей
- Cтруктура речення в англійській мові
- Модальні дієслова - англійська мова
- Англійський алфавіт для дітей
- Буква «А» англійського алфавіту
- Буква «B» англійського алфавіту
- Буква «C» англійського алфавіту
- Буква «D» англійського алфавіту
- Буква «E» англійського алфавіту
- Буква «F» англійського алфавіту
- Буква «G» англійського алфавіту
- Буква «H» англійського алфавіту
- Буква «I» англійського алфавіту
- Буква «J» англійського алфавіту
- Буква «K» англійського алфавіту
- Буква «L» англійського алфавіту
- Буква «M» англійського алфавіту
- Буква «N» англійського алфавіту
- Буква «O» англійського алфавіту
- Буква «P» англійського алфавіту
- Буква «Q» англійського алфавіту
- Буква «R» англійського алфавіту
- Буква «S» англійського алфавіту
- Буква «T» англійського алфавіту
- Буква «U» англійського алфавіту
- Буква «V» англійського алфавіту
- Буква «W» англійського алфавіту
- Буква «X» англійського алфавіту
- Буква «Y» англійського алфавіту
- Буква «Z» англійського алфавіту
- Англійська мова: словниковий запас
- Сім’я англійською мовою для дітей
- Іграшки англійською мовою
- Числа англійською мовою для дітей
- Тварини англійською мовою для дітей
- Шкільне приладдя англійською мовою
- Свята англійською мовою для дітей
- Погода та пори року на англійській мові
- Предмети одягу англійською мовою для дітей
- Меблі англійською мовою для дітей
- Частини тіла та зовнішність людини англійською
- Їжа англійською для дітей
- Захоплення та хобі англійською мовою
- Дні тижня та місяці англійською мовою для дітей
- Сторони світу англійською мовою для дітей
- Посуд англійською мовою для дітей
- Види спорту на англійській мові для дітей
- Транспорт англійською мовою для дітей
- Фрукти і овочі англійською мовою для дітей
- Професії англійською мовою для дітей
- Прийменники в англійській мові для дітей
- Порівняння довжини для дітей
- Одиниці вимірювання довжини для дітей
- Кольори англійською мовою для дітей
- Я досліджую світ
- Вивчення днів тижня
- Пори року та місяці для дітей
- Вчимо кольори для дітей
- Завдання на тему погода для дітей
- Завдання про тварин для дітей
- Завдання про рослини для дітей
- Завдання на тему космос для дітей
- Завдання на тему транспорт для дітей
- Завдання на тему професії для дітей
- Завдання на тему моя сім’я для дітей
- Завдання по темі екологія для дітей
- Пізнаю себе - завдання для дітей
- Завдання на тему довкілля для дітей
- Завдання з теми харчування для дітей
- Органи чуття – завдання для дітей
- Принципи здорового харчування
- Час доби – завдання для дітей
- Практичні завдання Вода
- Практичні завдання Календар
- Земля
- Країни світу
- Спорт
- Видатні постаті
- Материки та океани
- Птахи
- Практичні завдання Свійські тварини
- Практичні завдання Дикі тварини
- Практичні завдання Комахи
- Практичні завдання Мешканці морів та океанів
- Практичні завдання Овочі
- Практичні завдання Фрукти та ягоди
- Практичні завдання Дерева (Рослини лісу)
- Практичні завдання Квіти
- Практичні завдання Жива та нежива природа
- Українська мова та читання для дітей
- Письмо та правопис для дітей
- Написання слів для дітей
- Каліграфічні прописи українського алфавіту (прописні літери)
- Рими для дітей
- Читання по складах для дітей
- Синоніми та антоніми для дітей
- Завдання на вивчення букв для дітей
- Анаграми для дітей
- Кросворди для дітей
- Прописи друкованих літер українського алфавіту
- Розвиток зв’язного мовлення
- Фразеологізми для дітей
- Глухі та дзвінкі звуки для дітей
- Синоніми для дітей
- Слова протилежні за значенням (антоніми)
- Омоніми для дітей
- Голосні звуки для дітей
- Приголосні звуки для дітей
- Дзвінкі звуки для дітей
- Глухі звуки для дітей
- Шиплячі звуки для дітей
- Кросворди з картинками для дітей
- Класичні кросворди для дітей
- Головоломки українською мовою для дітей
- Ребуси для дітей
- Лабіринти з буквами для дітей
- Філворди для дітей
- Загадки для дітей
- Метаграми для дітей
- Логогрифи для дітей
- Чайнворди для дітей
- Будова слова - завдання для дітей
- Вчимось писати речення - завдання для дітей
- Розповідне речення
- Спонукальне речення
- Питальне речення
- Окличне речення
- Деформовані речення
- Схема речення
- Службові слова
- Головні члени речення
- Другорядні члени речення
- Розділові знаки
- Складне речення
- Складаємо речення
- Доповнити речення
- Вчимось писати історії
- Створюємо комікси - завдання для дітей
- Частини мови для дітей
- Прислівник для дітей
- Іменник для дітей
- Дієслова для дітей
- Прикметники для дітей
- Частина мови сполучник для дітей
- Прийменники для дітей
- Числівник – завдання для початкових класів
- Правопис для дітей
- Власні та загальні назви
- Списування речень
- М’який знак – завдання для дітей
- Апостроф – завдання для дітей
- Ненаголошені [е], [и] – завдання для дітей
- Подовження і подвоєння
- Префікси
- Суфікси для учнів початкових класів
- Частка «не» з дієсловами
- Перенос слів
- Буквосполучення -йо- -ьо-
- Чергування голосних
- Чергування приголосних звуків
- Пряме і переносне значення слів
- Тексти для списування
- Словникові слова
- Складне речення
- Практичні завдання Словосполучення
- Буквосполучення -дж- -дз-
- Літературне читання для дітей
- Техніки читання
- Тексти для читання
- Читацький досвід для дітей
- Практичні завдання Швидкочитання
- Читацька компетентність - завдання для дітей
- Літературні герої - завдання для дітей
- Словниковий запас
- Робота з джерелами інформації для дітей
- Займенник – завдання для дітей
- Практичні завдання Відмінювання іменників
- Практичні завдання Відмінювання прикметників
- Практичні завдання Відмінювання числівників
- Відмінювання та відмінки
- Наголос у словах
- Пряме і переносне значення слів
- Прописи слів друкованим шрифтом
- Прописи слів прописним шрифтом
- Вставити пропущені букви
- Списування слів для дітей
- Прислівʼя та приказки для дітей
- Шифри слів для дітей
- Практичні завдання Словосполучення
- Практичні завдання Значення слова
- Картки для розчитування
- Практичні завдання Поділ слів на склади
- Практичні завдання Висловлення думок (аргументація)
- Багатозначні слова для дітей
- Навчання дітей читання
- Звукова схема слова
- Практичні завдання Деформований текст
- Учимося описувати – завдання для дітей
- Учимося описувати властивості
- Учимося описувати дії – завдання для дітей
- Учимося описувати поняття – завдання для дітей
- Учимося описувати місця – завдання для дітей
- Учимося описувати книжки
- Учимося описувати стосунки у сім’ї
- Учимося описувати відчуття
- Учимося описувати характер
- Учимося описувати погоду
- Учимося описувати ситуації - завдання для дітей
- Учимося описувати значення слів - завдання для дітей
- Учимося описувати предмети - завдання для дітей
- Математика для дітей
- Фігури і геометрія для дітей
- Прописи цифр та чисел для дітей
- Вчимося визначати час за годинником
- Математичні головоломки для дітей
- Розмальовки з фігурами для дітей
- Малювання фігур по точках для дітей
- Об’ємні фігури для дітей
- Фігури в об’єктах для дітей
- Назви геометричних фігур для дітей
- Головоломки з фігурами для дітей
- Ознаки фігур для дітей
- Рівняння для початкових класів
- Японські кросворди для дітей
- Судоку для дітей
- Вимірювання та порівняння для дітей
- Дані, робота з даними для дітей
- Одниці вимірювання маси
- Вимірювання об’єму для дітей
- Інструменти вимірювання для дітей
- Одиниці вимірювання для дітей
- Задачі на швидкість та рух
- Одиниці вимірювання висоти
- Одиниці вимірювання площі – задачі для початкових класів
- Гроші для дітей
- Римські числа та цифри для дітей
- Розряди чисел
- Математичнні лабіринти для дітей
- Математичні ланцюжки для дітей
- Дії з іменованими числами
- Додавання і віднімання іменованих чисел
- Перетворення іменованих чисел
- Складені іменовані числа
- Порівняння іменованих числел
- Парні і непарні числа
- Прості рівняння
- Рівняння на дві дії для учнів НУШ
- Рівняння з дужками
- Рівняння на додавання і віднімання
- Рівняння на множення і ділення
- Складені рівняння
- Склад числа
- Практичні завдання Периметр
- Числовий промінь
- Діагностувальні роботи з математики
- Завдання та приклади на множення для дітей
- Таблиця множення для дітей
- Приклади на множення для дітей
- Письмове множення для дітей
- Таблиця множення на «2»
- Таблиця множення на «3»
- Таблиця множення на «4»
- Таблиця множення на «5»
- Таблиця множення на «6»
- Таблиця множення на «7»
- Таблиця множення на «8»
- Таблиця множення на «9»
- Невідомий множник
- Переставний закон множення
- Завдання та приклади на ділення для дітей
- Письмове ділення, ділення в стовпчик для дітей
- Приклади на ділення для дітей
- Множення і ділення іменованих чисел
- Невідоме ділене
- Невідомий дільник
- Завдання на віднімання для дітей
- Віднімання в межах 5
- Віднімання в межах 10
- Віднімання в межах 20
- Віднімання в межах 100
- Віднімання в картинках для дітей
- Віднімання в межах 1000 для дітей
- Віднімання в межах 1 млн – завдання для дітей
- Невідоме зменшуване
- Невідомий від’ємник
- Віднімання через розряд
- Практичні завдання Письмове віднімання
- Завдання на додавання для дітей
- Додавання за допомогою малюнків
- Додавання в межах 5 для дітей
- Додавання в межах 10 для дітей
- Додавання в межах 20 для дітей
- Невідомий доданок
- Додавання в межах 100 для дітей
- Додавання в межах 1000 для дітей
- Додавання в межах 1 мільйона - завдання для дітей
- Додавання через розряд
- Практичні завдання Письмове додавання
- Задачі з математики для дітей
- Задачі на дві дії для дітей
- Задачі на три дії для дітей
- Задачі на одну дію для дітей
- Задачі на спільну роботу
- Складені задачі для учнів НУШ
- Задачі на продуктивність праці
- Задачі на пропорційне ділення
- Задачі на різницеве порівняння
- Задачі на кратне порівняння
- Задачі на зведення до одиниці
- Задачі на дроби
- Задачі на четверте пропорційне
- Короткий запис задачі
- Обернені задачі для учнів НУШ
- Задачі на середнє значення
- Задачі на множення і ділення
- Задачі на додавання і віднімання
- Числа та цифри для дітей
- Прописи та розмальовки цифри «0» для дітей
- Прописи та розмальовки цифри 1 для дітей
- Прописи та розмальовки цифри 2 для дітей
- Прописи та розмальовки цифри 3 для дітей
- Прописи та розмальовки цифри 4 для дітей
- Прописи та розмальовки цифри 5 для дітей
- Прописи та розмальовки цифри 6 для дітей
- Прописи та розмальовки цифри 7 для дітей
- Прописи та розмальовки цифри 8 для дітей
- Прописи та розмальовки цифри 9 для дітей
- Числа від 10 до 20 для дітей
- Вчимося рахувати до 10
- Завдання для навчання дітей рахунку до 20-ти
- Вчимося рахувати
- Рахунок до 5 для дітей
- Рахунок до 50 для дітей
- Рахунок в межах 100 для дітей
- Аплікації для дітей
- Аплікації Тварини
- Аплікації Свята та дати
- Аплікації Транспорт
- Аплікації Водний світ
- Аплікації Рослини
- Аплікації Пори року
- Аплікації Квіти
- Аплікації Україна
- Аплікації Птахи
- Аплікації Космос
- Аплікації Безпека
- Аплікації За видами
- Аплікації Сюжетна аплікація
- Аплікації Рвана аплікація
- Аплікації З природних матеріалів
- Аплікації З пластиліну
- Аплікації З листя
- Аплікації З паперу
- Аплікації Різне
- Аплікації Світлофор
- Аплікації Літо
- Аплікації Різдво
- Аплікації Новий рік
- Аплікації Святий Миколай
- Аплікації День хліба
- Аплікації День миру
- Аплікації День козацтва
- Аплікації День вишиванки
- Аплікації Великдень
- Аплікації Продукти харчування
- Аплікації Парасолька
- Аплікації Одяг
- Аплікації Геометричні фігури
- Аплікації Веселка
- Аплікації Будинок
- Аплікації Корабель
- Аплікації Літак
- Аплікації Машина
- Аплікації Вантажівка
- Аплікації 8 березня
- Аплікації День матері
- Аплікації Мозаїка
- Аплікації Сніговик
- Аплікації Янгол
- Аплікації Ялинкова іграшка
- Аплікації Ялинка
- Аплікації Хустинка
- Аплікації Свічка
- Аплікації Санчата
- Аплікації Білочка
- Аплікації Ведмідь
- Аплікації Зайчик
- Аплікації Їжак
- Аплікації Лисичка
- Аплікації Пінгвін
- Аплікації Собака
- Аплікації Віночок
- Аплікації Писанка
- Аплікації Прапор
- Аплікації Рушник
- Аплікації Гарбуз
- Аплікації Гриб
- Аплікації Дерево
- Аплікації Сад
- Аплікації Ягоди
- Аплікації Годівничка
- Аплікації Синичка
- Аплікації Сонячна система
- Аплікації Снігур
- Аплікації Пейзаж
- Аплікації День Соборності України
- Аплікації Казки
- Аплікації Рукавичка
- Аплікації День Валентина
- Аплікації Комахи
- Аплікації Баран
- Аплікації Равлик
- Аплікації Метелик
- Аплікації Тюльпан
- Поробки для дітей
- Поробки Україна
- Поробки Миколай
- Поробки Осінь
- Поробки Зима
- Поробки Різдво
- Поробки Новий рік
- Поробки Космос
- Поробки Витинанки
- Поробки Весна
- Поробки Літо
- Поробки 8 березня
- Поробки Великдень
- Поробки День миру
- Поробки День матері
- Поробки День Землі
- Поробки День захисту дітей
- Поробки День захисника України
- Поробки День вчителя
- Поробки День вишиванки
- Поробки День Святого Валентина
- Поробки День батька
- Розвиток загальних компетенцій дитини
- Розвиток уяви у дітей
- Завдання на розвиток уваги у дітей
- Розвиток емоційного інтелекту у дітей
- Комп’ютерна грамотність для дітей
- Тайм менеджмент для дітей
- Завдання на тему «Здоров’я» для дітей
- Фінансова грамотність для дітей
- Пишемо плани на рік – завдання для дітей
- Плани на день – завдання для дітей
- Плануємо відпочинок – завдання для дітей
- Складаємо план дій – завдання для дітей
- Вчимося ставити цілі – завдання для дітей
- Навчання дітей безпеки
- Комунікація і спілкування для дітей
- Практичні завдання Портфоліо учня
- Плани на тиждень
- Нейровправи для дітей
- Практичні завдання Розвиток мовлення
- Практичні завдання Пожежна безпека
- Практичні завдання Безпека на дорозі
- Практичні завдання Знайди відмінності
- Практичні завдання Звуконаслідування
- Практичні завдання Особиста гігієна
- Малювання для дітей
- Симетрія для дітей
- Завдання домалювати малюнок для дітей
- Малювання за інструкцією для дітей
- Дзеркальне малювання для дітей
- Малювання однією лінією для дітей
- Малювання листівок для дітей
- Малювання за точками для дітей
- Копіювання малюнків для дітей
- Малювання по клітинках для дітей
- Уяви та намалюй – завдання для дітей
- Практичні завдання Графічні диктанти
- Пальчикове малювання для дітей
- Розмальовки для дітей
- Розмальовки тварин для дітей
- Розмальовки фруктів і овочів для дітей
- Розмальовки машин і техніки для дітей
- Розмальовки казок для дітей
- Розмальовки для хлопчиків
- Розмальовки для дівчат
- Розмальовки одягу для дітей
- Розмальовки пори року для дітей
- Розмальовки дерев для дітей
- Розмальовки птахів для дітей
- Розмальовки їжі для дітей
- Розмальовки комах для дітей
- Розмальовки людей і зовнішності для дітей
- Розмальовки країн і прапорів для дітей
- Розмальовки на тему погода для дітей
- Розмальовки чудеса світу для дітей
- Розмальовки квітів для дітей
- Розмальовки за цифрами для дітей
- Розмальовки букв алфавіту для дітей
- Новорічні розмальовки для дітей
- Динозаври – навчальні розмальовки для дітей
- Тематичні завдання для дітей
- Завдання на Новий рік для дітей
- Завдання на Хелловін для дітей
- Завдання на Великдень для дітей
- Завдання на День матері для дітей
- Завдання на день народження для дітей
- Завдання на Різдво для дітей
- Завдання на День Незалежності для дітей
- Завдання на День святого Валентина для дітей
- Завдання на День захисника України для дітей
- Завдання на 8 березня для дітей
- Завдання на тему «Зима» для дітей
- Завдання на тему «Весна» для дітей
- Завдання на тему «Літо» для дітей
- Завдання на тему «Осінь» для дітей
- Завдання на День вишиванки для дітей
- Асоціації для дітей
- Завдання на День батька для дітей
- Практичні завдання Україна
- Практичні завдання День доброти
- Практичні завдання День учителя
- Практичні завдання День святого Миколая
- Практичні завдання Інші свята та дати
- Практичні завдання Всесвітній день дитини
- Практичні завдання День захисту тварин
- Практичні завдання День усмішки
- Практичні завдання День кота
- Практичні завдання День жертв Голодомору
- Практичні завдання День Землі
- Практичні завдання День соборності
- Практичні завдання День хустки
- Практичні завдання День домашніх тварин
- Практичні завдання День миру
- Український алфавіт для дітей
- Буква «А» українського алфавіту
- Буква «Б» українського алфавіту
- Буква «В» українського алфавіту
- Буква «Г» українського алфавіту
- Буква «Ґ» українського алфавіту
- Буква «Д» українського алфавіту
- Буква «Е» українського алфавіту
- Буква «Є» українського алфавіту
- Буква «Ж» українського алфавіту
- Буква «З» українського алфавіту
- Буква «И» українського алфавіту
- Буква «І» українського алфавіту
- Буква «Ї» українського алфавіту
- Буква «Й» українського алфавіту
- Буква «К» українського алфавіту
- Буква «Л» українського алфавіту
- Буква «М» українського алфавіту
- Буква «Н» українського алфавіту
- Буква «О» українського алфавіту
- Буква «П» українського алфавіту
- Буква «Р» українського алфавіту
- Буква «С» українського алфавіту
- Буква «Т» українського алфавіту
- Буква «У» українського алфавіту
- Буква «Ф» українського алфавіту
- Буква «Х» українського алфавіту
- Буква «Ц» українського алфавіту
- Буква «Ч» українського алфавіту
- Буква «Ш» українського алфавіту
- Буква «Щ» українського алфавіту
- Буква «Ь» українського алфавіту
- Буква «Ю» українського алфавіту
- Буква «Я» українського алфавіту
- Завдання на логіку для дітей
- Знайди тінь – дидактичні ігри для дітей
- Логічні задачі для дітей
- Завдання на аналогії для дітей
- Частини цілого для дітей
- Логічні ігри для дітей
- Правильний порядок для дітей
- Завдання на класифікацію предметів для дітей
- Головоломки на логіку для дітей
- Шифри і коди для дітей
